《方程的意义》教学设计
一、教学内容
人教版五年级上册第62-63页内容。
二、 教材分析
五年级上册《方程的意义》教学分析《方程的意义》是人教课标版五年级上册第五单元的内 容,它是学生学习了四年用算术思想解题后,在掌握了用字母表示数的基础上进行教学的,同时 又是即将学习解方程的基础。对于儿童来说是一堂全新的数学概念课,也是数学思维的一种提 升。因为学生解决实际问题的工具,从列出算式解发展到列出方程解,从未知数只是所求结果到
未知数参与运算,思维空间增大了,更是数学思想方法上的一次飞跃。
方程是解决问题的重要工具, 含有未知数的等式叫方程。 这是大家非常熟悉的对于方程的 定义,但实际上,学习方程仅仅知道这个定义没有多大价值。学习方程的价值在于会用方程解决 问题,逐步学会运用代数的方法思考问题,即培养学生代数思维的能力,这一切离不开方程思想
的渗透。方程思想的核心在于建模和化归(转化)。
本节课并不是把知识的教学作为唯一的教学目标,而是以这一内容为切入点,适时培养学生的
观察和概括能力,通过分类和再分类,初步建立数学分类思想和集合的思想。
所以: 教学设计的整体构思:
一、数学问题生活化,帮学生建立模型,培养学生的符号感。
二、 不同深度的分类活动,让学生体会分类的真正含义。
三 .学情分析
《方程的意义》 一课是人教版小学数学五年级上册第五单元第二节的内容。学生在《方程的 意义》之前,在一、二年级的数学学习中均有填算式中的括号,也就是未知数,对于方程的意义 有了一定的知识渗透,在本单元中,学生已经学习了用字母表示数,表示数量,表示数量间的关 系,都与本节课有着密切的关系。而方程这部分知识,在初等代数中占有重要的地位,对于小学 生来说,从具体事物的个数抽象出数是认识上的一个飞跃和,现在由具体的、确定的数过渡到用 字母表示抽象的、可变的数,更是认识上的一个飞跃。而且在用字母表示未知数的基础上,使学
生解决实际问题的数学工具,从列出算式发展到列出方程解,这又是数学思想方法认识上的一次
飞跃,它将使学生运用数学知识解决实际问题能力提高到一个新的水平。方程这部分的学习,能 使学生摆脱算术思维方法中的某些局限性,为进一步学习代数知识帮好认识的准备和铺垫。学生 从算术方法解决问题到代数方法解决问题的过渡,这节课的概念学习也是后面学习解方程的方法、
用方程解决问题的基础,因此,在教学中起着承上启下的作用。
四 .教学目标
1、通过观察天平平衡体会并找出等量关系,写出等式和含有未知数的等式,使学生经历从
生活原型到方程概念的建立过程,体会方程是一个用数学符号提炼现实生活中的特定关系的过程。
2、在观察天平不平衡到平衡的过程中得到一些数学式子,通过对这些式子的分类再分类的
过程,让学生感受分类思想,理解并掌握方程的意义,弄清方程与等式间的联系与区别。
3、在观察天平的过程中,培养学生认真观察,用数学思维思考生活中的问题的学习品质。
五、教学重点
理解方程的含义,会用方程表示简单情景中的等量关系。
六、 教学难点
用方程的思想刻画简单情境中的等量关系。
七、教学准备
多媒体课件。
八 、教学流程
(一)感受等式,理解等式。
利用天平的直观性引导学生将生活中的情景用等式或不等式表达出来。
(二)对式子进行分类。
在引导学生想法的前提下,让学生自主对式子进行分类。
(三)引入方程概念。
(四)理解方程意义。
借助天平呈现出简单的相等的情景,让学生经历将生活情境转变成数学语言的过程。
(五)联系生活实际,感受方程的价值。
(六)课堂小结。
九、 教学过程
(一)感受等式,理解等式。
1、 出示天平的图片,让同学们了解天平的基本功能,知道只有当两边放的物体重量相等时
天平才会平衡。
师:我们一起用天平来称东西。
出示180克的苹果和120克的香蕉,300克的砝码。
让孩子用数学的语言来表达。
120+180=300
师:教师用图片展示出另外一个不知道质量的苹果,可能出现的哪些情况,然后提问那么天
平会怎样?
生:平衡。
师:也就是说一个苹果和一个香蕉的质量和等于300克,你能否用一个数学式子表示出这种
相等的关系?
生:120+a=300
生:不平衡
120+a>300 或120+a<300
师:香蕉拿走,放入3个相同质量的苹果,天平平衡,怎么表示
生:3x+300
通过继续用天平称,得出一系列的式子:20+30=50 a+30+50
Y+30<50 x=30+50 x+30>50......
(设计意图:利用直观的天平平衡,很容让学生初步感知物体质量之间自然产生的相等关系,
等式是方程的生长点。而利用连续进球个数的数量不确定,则将未知数引入到式子中。)
(二)对式子分类
我们已经列出了许多的式子,还记得老师说过,数量之间的关系可以分为相等关系和不相等
关系两大类,那么黑板上有这么多表示不同数量关系的式子,你能将这些式子分成两类吗?
【预设】学生将等于号的式子分为一类,大于号或小于号的式子分为一类。
设计意图: “数量之间的关系可以分为相等关系和不相等关系两大类”这句话需要进行强 调,否则学生容易将式子分为三类,即大于号一类,小于号一类,等于号一类,我们不反对学 生有其他多样的想法,但我们应尽可能的提高课堂的效率,我认为,这并没有抑制学生的多样
性想法,而是在引导他们的想法。
教师继续引导学生按式子中是否含有字母对黑板上的式子进一步分类,最终将所有式子分为
三类,并请学生说出每一类式子的特征:不含字母的等式,不等式,含有字母的等式。
设计意图:没有把“方程就是含有未知数的等式”这一概念硬塞给学生,而是让学生在自 主探索的过程中,发现规律,研究知识,通过学生自己对式子进行分类,培养了学生的分类意
识,又为引出方程概念做好了铺垫。
(三)引入方程概念
师:今天我们要研究的就是其中的一类,含有字母的等式,这类式子有一个好听的名字叫做
方程。
请同学们说说其他三类式子为什么不叫方程,强化方程概念。
并且带领学生识别方程。(课件练习题)
(四)理解方程的意义
幻灯片出示练习题。
1. 有2000毫升水能倒满两个水壶,剩下200毫升倒入水杯,能列出方程式吗?
师:看着这道题,调出你心中的天平,左边有2000毫升水,右边是空的,要想平衡,怎么 办?好,老师开始往右边加水,呼啦, 一水壶,平了吗?再来一水壶,平了吗?再给你200
毫升,平了吗?好,根据分析,称出方程式来。
生:x+x+200=2000
2.3个猕猴桃的质量一共是500克,每个猕猴桃的质量是多少?列出方程式。
师:谁能根据分析给这道题也列出方程来?
生:3x=500
设计意图:在引入方程的概念后,利用直观的天平构建生活中的相等情景,引导学生经历 从生活语言描述事件到用数学语言描述等式,在用方程表示等量关系的过程中,完成将现实世
界中的等量关系数学化、符号化,最后一步的设计,巩固了学生对方程概念的理解, 一架天平,
一个难点, 一次突破。
(五)感受方程的价值
写方程编故事
38+x=100
(六)课堂小结
通过这节课的学习,你有什么收获?今天所学的知识将是后面学习解方程、用方程解决问题
的基础,以后可以用这方面的知识解决算术方法难以解决的问题。
十、 板书设计
称出来的方程
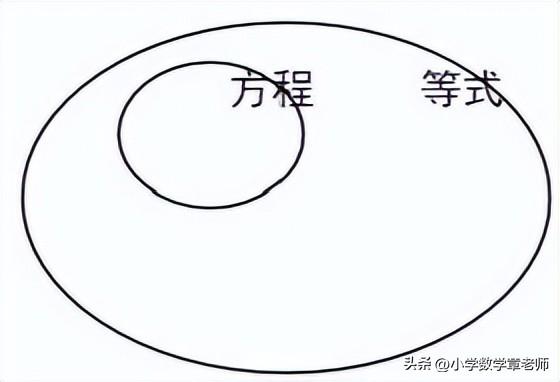
含有未知数的等式叫做方程
十一、设计特色
(一)一架天平架起通过难点的桥梁
教师提供“用天平秤”这一素材,既符合学生的经验,又恰如其分地体现了方程的本质特征
——等量关系,使学生借用生活经验与感受构建起对方程等量关系的认同。
“在用方程思想刻画简单情景中的等量关系”这一教学难点的处理上,巧妙的递给学生一根 吸管,学生自然会想到用吸管吸去杯中的饮料,而吸去饮料的重量则用未知数来表示,借助多媒 体的演示,天平随着杯中饮料的减少而渐渐平衡,当达到平衡点时,未知数有了,相等关系有了,
方程自然就有了。
(二)引导想法,放手学生,提高课堂效率。
在对式子进行分类时,先对学生的想法进行引导,然后再把分类的权力留给学生,放手让学 生自己去发现,同时培养了学生的分类意识及思想。没有把概念硬塞给学生,而是让学生自己在 分类的过程中发现规律,继而呈现出方程的概念。通过对学生想法的引导,学生会快速按照“是
否相等”这一标准对式子进行分类,这样就达到了即引导想法,同时又让学生自主探索的目的,
